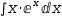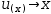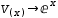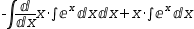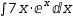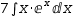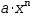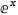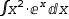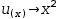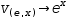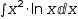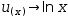4.4.1 Integration by Parts

Integration by parts is used when the integrand contains a product expression. The transformation does not perform a complete integration; rather it rearranges the expression to contain unsimplified expressions that in turn contain integration. The technique transforms ∫u(x)⋅v(x) ⅆx into u(x)⋅∫v(x) ⅆx-∫ⅆu(x)ⅆx⋅∫v(x) ⅆx ⅆx. Try this for 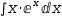∫x⋅ⅇ^x ⅆx where 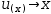u(x)→x and 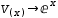v(x)→ⅇ^x. You get 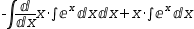-∫ⅆxⅆx⋅∫ⅇ^x ⅆx ⅆx+x⋅∫ⅇ^x ⅆx. To proceed, you have to select and simplify individual derivatives and integrals in the expression.

Integration by parts is not needed for a simple product whose first term is constant. Note, however, the different results when integrating 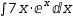∫7⋅x⋅ⅇ^x ⅆx and 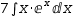7⋅∫x⋅ⅇ^x ⅆx. It is always best to rearrange the integrand so constants appear outside the integral.

The choice of which of the two product terms should be u and which should be v is made by selection terms according to the LIATE heuristic. LIATE is an acronym for a scheme of ordered categorizations.

• L - logarithms
• I - inverse trigonometric functions: arcsin, arccos, etc
• A - algebraic expressions of the form 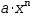a⋅x^n – essentially, polynomials
• T - trigonometric functions: sin, cos, etc
• E - exponential: expressions of the form 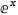ⅇ^x

The LIATE heuristic chooses as u the expression with an earlier LIATE category and chooses as v the expression with a later category.

For example, from 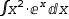∫x^2⋅ⅇ^x ⅆx the heuristic chooses 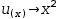u(x)→x^2 and 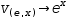v(e, x)→e^x, while from 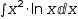∫x^2⋅ln x ⅆx it chooses 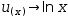u(x)→ln x and v(x)→x^2.